QNLP Namespace Reference

Namespaces
	encoding
	io
	proc
	tagging

Data Structures
class	Arithmetic
	Class definition for bit-wise summation and subtraction of qubits. More...
class	BitGroup
	Class definition for bit-wise grouping in register. More...
class	CorpusUtils
class	DBHelper
class	Diffusion
	Class definition for applying Grover diffusion to a marked register. More...
class	EncodeBinIntoSuperpos
	Definition of class to encode a binary string represented by an integer into a superposition of states. More...
class	GateCache
	Class to cache intermediate matrix values used within other parts of the computation. Heavily depended upon by NCU to store sqrt matrix values following Barenco et al. (1995) decomposition. More...
struct	GateMetaData
	Meta container object for gate caching. More...
struct	GateMetaDataHasher
	Hashing function for GateMetaData objects, to allow storage in unordered_map. Taken from default docs example. More...
class	GateWriter
class	HammingDistance
	Class definition for implementing the Hamming distance routine along with controlled Y rotations to encode the Hamming distance into the states' amplitudes. More...
class	IntelSimulator
	Class definition for IntelSimulator. The purpose of this class is to map the functionality of the underlying quantum simulator to this class so that it can be used as the template for the CRTP templated SimulatorGeneral class. More...
class	ISimulator
class	NCU
	Class definition for applying n-qubit controlled unitary operations. More...
class	Oracle
	Class definition for defining and applying an Oracle. More...
class	QFT
	Class definition for performing quantum forward and inverse Fourier transforms. More...
class	SimulatorGeneral
	CRTP defined class for simulator implementations. More...
class	Singleton
	Follows the Meyers singleton pattern, allowing thread-safe access to singleton object. More...

Functions
template<class fpType >
bool	fpComp (fpType theta0, fpType theta1)
	Comparison of floating point values within the given machine epsilon. More...
template<class Mat2x2Type >
const Mat2x2Type	matrixSqrt (const Mat2x2Type &U)
	Calculates the unitary matrix square root (U == VV, where V is returned) More...
template<class Mat2x2Type >
Mat2x2Type	adjointMatrix (const Mat2x2Type &U)
	Function to calculate the adjoint of an input matrix. More...

Variables
string	name

Function Documentation

adjointMatrix()

template<class Mat2x2Type >

Mat2x2Type QNLP::adjointMatrix

(

const Mat2x2Type &

U

)

Function to calculate the adjoint of an input matrix.

Template Parameters

Type	ComplexDP or ComplexSP

Parameters

U	Unitary matrix to be adjointed

Returns

openqu::TinyMatrix<Type, 2, 2, 32> U^{\dagger}

Definition at line 54 of file mat_ops.hpp.

                                                 {
        Mat2x2Type Uadjoint(U);
        std::complex<double> tmp;
        tmp = Uadjoint(0,1);
        Uadjoint(0,1) = Uadjoint(1,0);
        Uadjoint(1,0) = tmp;
        Uadjoint(0,0) = std::conj(Uadjoint(0,0));
        Uadjoint(0,1) = std::conj(Uadjoint(0,1));
        Uadjoint(1,0) = std::conj(Uadjoint(1,0));
        Uadjoint(1,1) = std::conj(Uadjoint(1,1));
        return Uadjoint;
    }

References QNLP.tagging.tag_file::tmp.

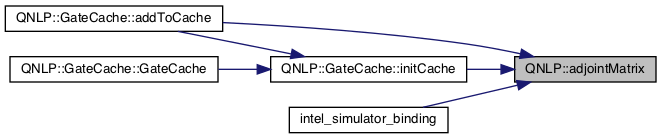
Referenced by QNLP::GateCache< SimulatorType >::addToCache(), QNLP::GateCache< SimulatorType >::initCache(), and intel_simulator_binding().

Here is the caller graph for this function:

fpComp()

template<class fpType >

bool QNLP::fpComp ( fpType  theta0, fpType  theta1  )

inline

Comparison of floating point values within the given machine epsilon.

Template Parameters

fpType

Floating point type (float, double)

Parameters

theta0	First parameter to compare
theta1	Second parameter to compare

Returns

true Abs value of the difference of params is less than given eps

false Abs value of the difference of params is greater than given eps

Definition at line 38 of file GateCache.hpp.

                                                     {
        return std::fabs(theta0 - theta1) < std::numeric_limits<fpType>::epsilon();
    }

matrixSqrt()

template<class Mat2x2Type >

const Mat2x2Type QNLP::matrixSqrt

(

const Mat2x2Type &

U

)

Calculates the unitary matrix square root (U == VV, where V is returned)

Template Parameters

Type	ComplexDP or ComplexSP

Parameters

U	Unitary matrix to be rooted

Returns

Matrix V such that VV == U

Definition at line 26 of file mat_ops.hpp.

                                                    {
        Mat2x2Type V(U);
        std::complex<double> delta = U(0,0)*U(1,1) - U(0,1)*U(1,0);
        std::complex<double> tau = U(0,0) + U(1,1);
        std::complex<double> s = sqrt(delta);
        std::complex<double> t = sqrt(tau + 2.0*s);

        //must be a way to vectorise these; TinyMatrix have a scale/shift option?
        V(0,0) += s;
        V(1,1) += s;
        std::complex<double> scale_factor(1.,0.);
        scale_factor /= t;
        V(0,0) *= scale_factor; //(std::complex<double>(1.,0.)/t);
        V(0,1) *= scale_factor; //(1/t);
        V(1,0) *= scale_factor; //(1/t);
        V(1,1) *= scale_factor; //(1/t);

        return V;
    }

Variable Documentation

name

string QNLP.name

Definition at line 1 of file __init__.py.