Calculation Example

Calculation Example#

The following tutorial shows how to use qse to run a calculation. We use pulser here for the backend.

import matplotlib.pyplot as plt
import numpy as np
import qse
import pulser

Create a 2D square lattice#

omega_max = 2.0 * 2 * np.pi  # rad/µs
rabi_frequency = omega_max / 2.0  # rad/µs

# Now we generate the qbits object that represents a 2D lattice.
# Keeping the lattice spacing a bit below the blockade radius keeps
# the nearest neighbours antiferromagnetic.
blockade_radius = pulser.devices.MockDevice.rydberg_blockade_radius(
    rabi_frequency
)  # in µm
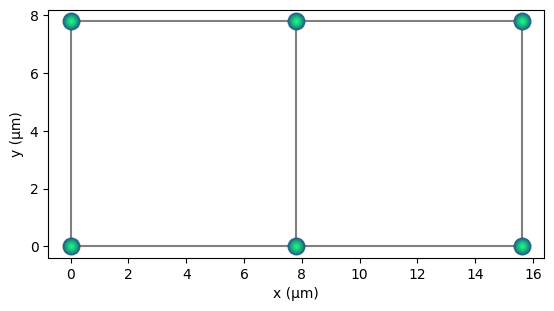
q2d = qse.lattices.square(
    lattice_spacing=0.8 * blockade_radius, repeats_x=3, repeats_y=2
)

q2d.draw(radius="nearest", units="µm")
../_images/aca6c9f6435d0f0c39fe13cf8e9811318c718b305bf39375e036c92e441a548a.png

Create the hamiltonian#

delta_0 = -6 * rabi_frequency  # ns
delta_f = 2 * rabi_frequency  # ns
t_rise = 252  # ns
t_fall = 500  # ns
t_sweep = (delta_f - delta_0) / (2 * np.pi * 10) * 1000  # ns

# up ramp, constant, downramp waveform
amplitude_afm = pulser.CompositeWaveform(
    pulser.waveforms.RampWaveform(t_rise, 0.0, omega_max),
    pulser.waveforms.ConstantWaveform(t_sweep, omega_max),
    pulser.waveforms.RampWaveform(t_fall, omega_max, 0.0),
)

# corresponding waveform for detuning
detuning_afm = pulser.CompositeWaveform(
    pulser.waveforms.ConstantWaveform(t_rise, delta_0),
    pulser.waveforms.RampWaveform(t_sweep, delta_0, delta_f),
    pulser.waveforms.ConstantWaveform(t_fall, delta_f),
)

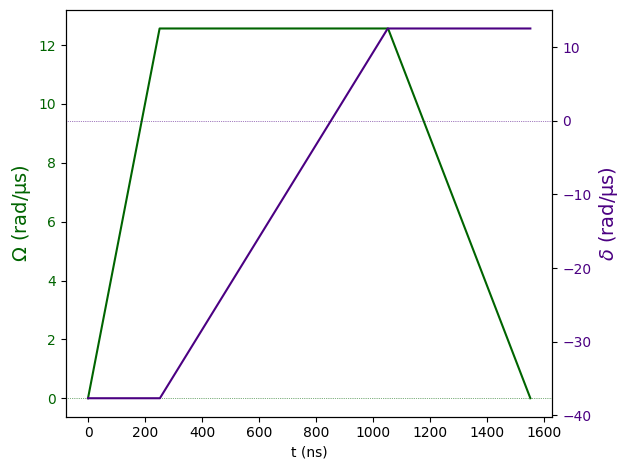
pulser.Pulse(amplitude=amplitude_afm, detuning=detuning_afm, phase=0.0).draw()
../_images/e5de594c59d1f07c71dbac6b12fa58792294681aa21a258d85016ee8cffa510f.png

Set up the calculator and run the job#

pcalc = qse.calc.Pulser(qbits=q2d, amplitude=amplitude_afm, detuning=detuning_afm)
pcalc.build_sequence()
pcalc.calculate()

10.1%. Run time:   0.00s. Est. time left: 00:00:00:00

20.0%. Run time:   0.01s. Est. time left: 00:00:00:00

30.0%. Run time:   0.01s. Est. time left: 00:00:00:00

40.0%. Run time:   0.01s. Est. time left: 00:00:00:00

50.0%. Run time:   0.01s. Est. time left: 00:00:00:00

60.1%. Run time:   0.02s. Est. time left: 00:00:00:00

70.0%. Run time:   0.02s. Est. time left: 00:00:00:00

80.0%. Run time:   0.02s. Est. time left: 00:00:00:00

90.0%. Run time:   0.03s. Est. time left: 00:00:00:00

100.0%. Run time:   0.03s. Est. time left: 00:00:00:00

Total run time:   0.03s
time in compute and simulation = 0.0575106143951416 s.

Sample the result#

count = pcalc.results.sample_final_state()

most_freq = {k: v for k, v in count.items() if v > 10}
plt.bar(list(most_freq.keys()), list(most_freq.values()))
plt.xticks(rotation="vertical")
plt.ylabel("Count")
plt.show()
../_images/a228c7c781b28265635473b05a632afa386dcc3764eb50d08278b325c6d58a96.png

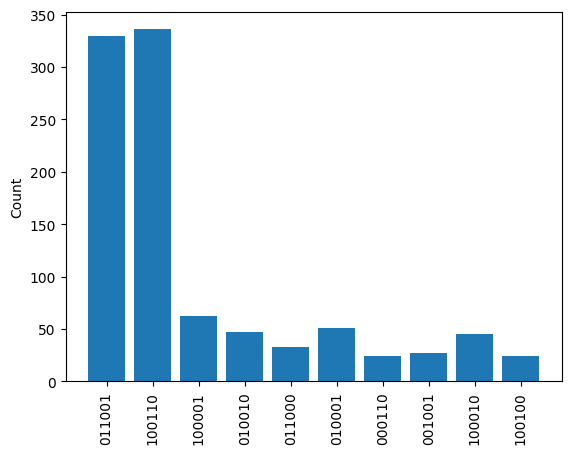
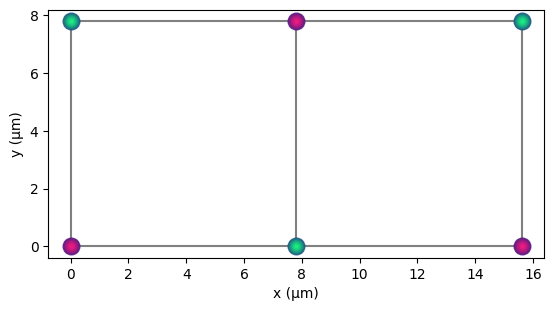
The states 011001 and 100110 are the most prevalent, we can visualise them using the colouring parameter in draw. We see that they correspond to anti-ferromagnetic orderings.

q2d.draw(radius="nearest", colouring="011001", units="µm")
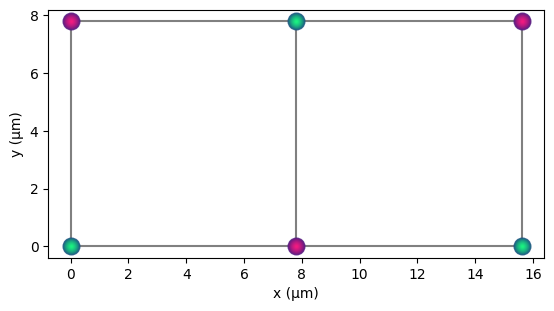
../_images/5843ff0f3c508727bcacdb74ccfa0524bd498d1e4e74a5fe1d8c582e4b0e931c.png 
q2d.draw(radius="nearest", colouring="100110", units="µm")
../_images/d1861033eb9711edb24ea31f90a7cf04af775b1cd16a6fdb5e46a39239a15fb5.png

Version#

qse.utils.print_environment()

Python version: 3.12.12
qse version: 1.0.3
Contents