QNLP.encoding.obrien.OBrienEncoder Class Reference

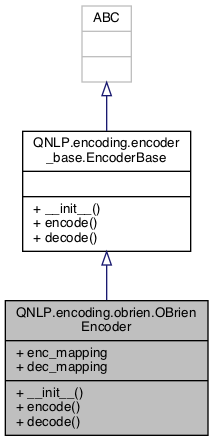
Inheritance diagram for QNLP.encoding.obrien.OBrienEncoder:

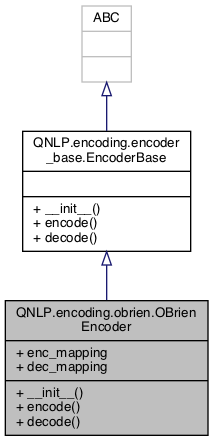
Collaboration diagram for QNLP.encoding.obrien.OBrienEncoder:

Public Member Functions
def	__init__ (self)
def	encode (self, bin_val)
def	decode (self, bin_val)

Data Fields
	enc_mapping
	dec_mapping

Detailed Description

O'Brien encoding scheme. Adapated from example on http://www.ahok.de/en/hoklas-code.html
Triangle stepping encoding distances when excluding first and last bits.
For simplicity, assumes 8 unique binary patterns (aka bases).
For bitstrings of length 4, the encoding schemes is defined as:

0 -> 0000
1 -> 0001
2 -> 0011
3 -> 0010
4 -> 0110
5 -> 1110
6 -> 1010
7 -> 1011
8 -> 1001
9 -> 1000

for a total of 10 unique patterns. If we ignore patterns 0000, and 1000 
we can have unity incremented pairwise Hamming distances between 0001 
and others up to 1110, and decremented thereafter. This leaves us with 8
unique bitstrings. Assuming the graph-problem for basis ordering offers
a Hamiltonian path, we can (possibly) use this pattern to better represent
the distances between words.

Definition at line 3 of file obrien.py.

Constructor & Destructor Documentation

__init__()

def QNLP.encoding.obrien.OBrienEncoder.__init__

(

self

)

Reimplemented from QNLP.encoding.encoder_base.EncoderBase.

Definition at line 29 of file obrien.py.

    def __init__(self):
        self.enc_mapping = { 1 : 1, 2 : 3, 3 : 2, 4 : 6, 5 : 14, 6 : 10, 7 : 11, 8 : 9 }
        self.dec_mapping = { v:k for k,v in self.enc_mapping.items() }

Member Function Documentation

decode()

def QNLP.encoding.obrien.OBrienEncoder.decode	(		self,
			bin_val
	)

Reimplemented from QNLP.encoding.encoder_base.EncoderBase.

Definition at line 39 of file obrien.py.

    def decode(self, bin_val):
        val_offset = bin_val + 1
        if val_offset not in self.dec_mapping:
            raise(ValueError("Decoding index value not within expected range. Value={}".format(val_offset)))
        return self.dec_mapping[val_offset]

References QNLP.encoding.obrien.OBrienEncoder.dec_mapping.

encode()

def QNLP.encoding.obrien.OBrienEncoder.encode	(		self,
			bin_val
	)

Reimplemented from QNLP.encoding.encoder_base.EncoderBase.

Definition at line 33 of file obrien.py.

    def encode(self, bin_val):
        val_offset = bin_val + 1
        if val_offset not in self.enc_mapping:
            raise(ValueError("Encoding index value not within expected range. Value={}".format(val_offset)))
        return self.enc_mapping[val_offset]
    

References QNLP.encoding.obrien.OBrienEncoder.enc_mapping.

Field Documentation

dec_mapping

QNLP.encoding.obrien.OBrienEncoder.dec_mapping

Definition at line 31 of file obrien.py.

Referenced by QNLP.encoding.obrien.OBrienEncoder.decode(), and QNLP.encoding.simple.SimpleEncoder.decode().

enc_mapping

QNLP.encoding.obrien.OBrienEncoder.enc_mapping

Definition at line 30 of file obrien.py.

Referenced by QNLP.encoding.obrien.OBrienEncoder.encode().

---

The documentation for this class was generated from the following file:

• /Users/mlxd/Desktop/intel-qnlp-rc2/modules/py/pkgs/QNLP/encoding/obrien.py