Generating Lattices

Generating Lattices#

We have several functions in the qse.lattices submodule to directly generate known lattices and geometries.

import numpy as np
import qse

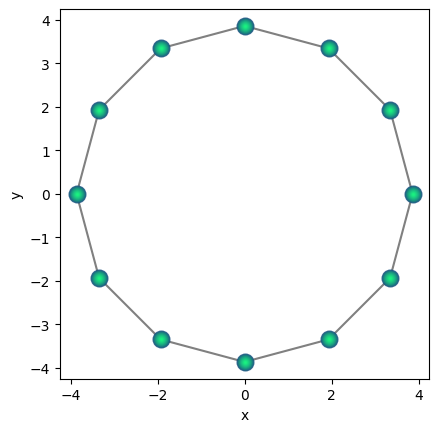
Ring geometry#

qring = qse.lattices.ring(spacing=2.0, nqbits=12)
qring.draw(radius="nearest")
../_images/7d662296522ec05ae2d54994c021417d68a8b096fe00eb27f6df9bcc83173372.png

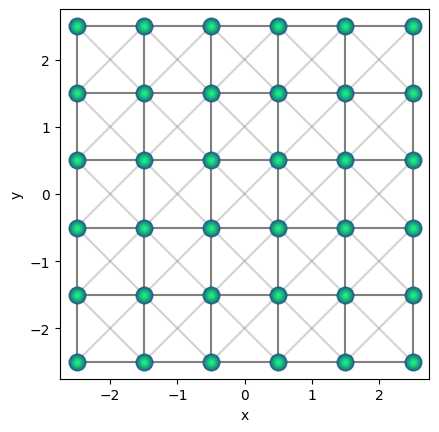
Square lattice#

qsquare = qse.lattices.square(1, repeats_x=6, repeats_y=6)
qsquare.set_centroid(0.0)
qsquare.draw(radius=2)
../_images/419a1bb16d6c632463e335a0d58cce324d6e8726c3b1cb51f6dde63de5975e23.png

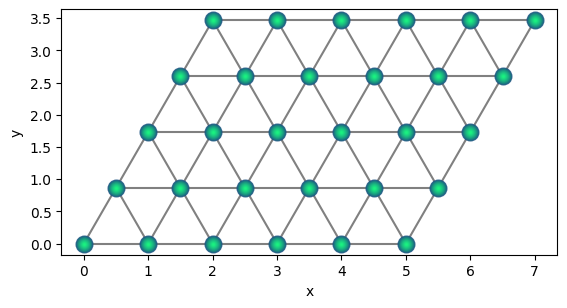
Triangular lattice#

qtriangle = qse.lattices.triangular(1, repeats_x=6, repeats_y=5)
qtriangle.draw(radius="nearest")
../_images/e51ff98fc9906db36bd5013810b2384fb543b1d865884434c92cf69f0321df1f.png

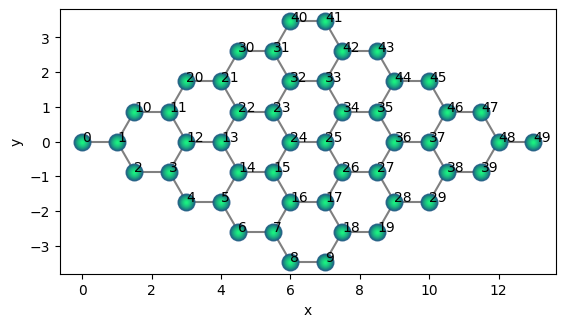
Hexagonal lattice#

qhexagon = qse.lattices.hexagonal(1, repeats_x=5, repeats_y=5)
qhexagon.draw(radius="nearest", show_labels=True)
../_images/a2ce06fa4adabd864a2bfd81df1630e72f979a74b1bfc096f9523b2bc90c40a9.png 
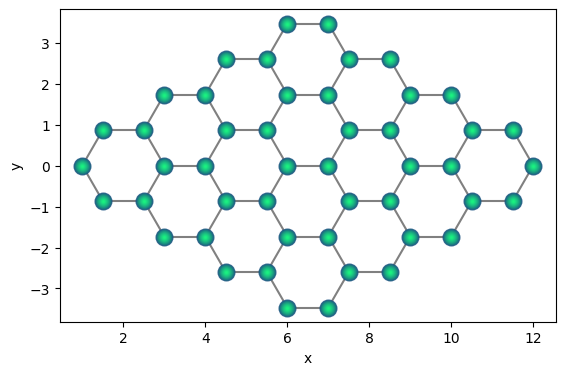
del qhexagon[[0, 49]]
qhexagon.draw(radius="nearest")
../_images/639fb9a9e1ee1d2b18966311555c187f0764c40582de480ca8ac96292240b6b7.png

Kagome lattice#

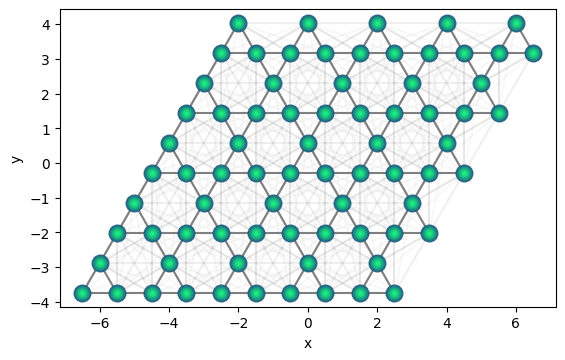
qkagome = qse.lattices.kagome(1, repeats_x=5, repeats_y=5)
qkagome.set_centroid(0.0)
qkagome.draw(radius=3)
../_images/9fcd5f2d50ddaf5974b5ce132f0acc859d7c35629d797ee078c957e08494c164.png

Constructing lattices via lattice vectors#

Rectangluar lattice#

spacing = 1.0
cell = spacing * np.array([[2.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 0.0]])

# qbits object with one qubit at origin
q_unit = qse.Qbits(positions=np.zeros((1, 3)), cell=cell)

# now repeat the pattern to get lattice of desired size
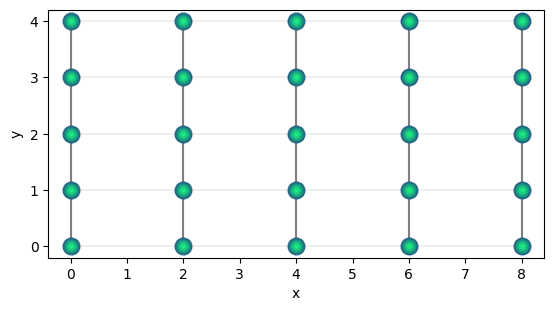
qrectangle = q_unit.repeat((5, 5, 1))
qrectangle.draw(radius=2)
../_images/6f84dc054faace2a14fa7538279d23d7d80446dfb656966c0b0fec3a97d1c354.png

Simple Cubic lattice#

spacing = 1.0
cell = spacing * np.array([[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0]])

# qbits object with one qubit at origin
q_unit = qse.Qbits(positions=np.zeros((1, 3)), cell=cell)

# now repeat the pattern to get lattice of desired size
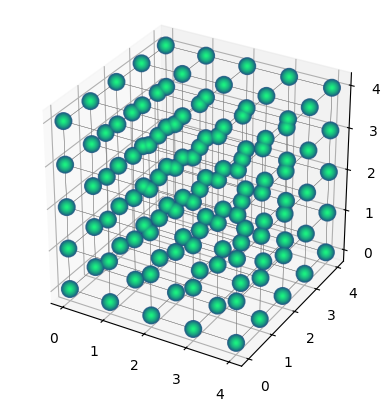
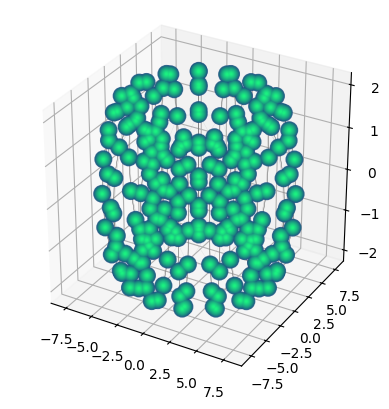
qsquare = q_unit.repeat((5, 5, 5))
qsquare.draw(radius="nearest")
../_images/31db55db4858564e94555e4647464544144b34586efbd20d52310fe7103fffa0.png

Some special geometries#

Torus geometry#

qtorus = qse.lattices.torus(n_outer=15, n_inner=15, inner_radius=2.0, outer_radius=6.0)
qtorus.draw(radius=2.0)
../_images/76c9ea11087411a3e629627d15920bf3786685f0376d647d21d3cb3c844a1840.png

Version#

qse.utils.print_environment()

Python version: 3.12.3
qse version: 0.2.24
Contents