Lecture 4: Mathematical framework for Quantum Computing

Lecture 4: Mathematical framework for Quantum Computing#

Warning

These lecture notes are a work in progress and are not a replacement for watching the lecture video, it’s intended to be a supplementary reading after watching the lecture

Learning outcomes

In this lecture we connect the mathematical framework of vector spaces and operators to the physical reality of quantum computing.

Postulates of Quantum Physics#

Let us go through some of the building blocks of quantum mechanics, and see how the required mathematical framework emerges.

Uncertainty Principle#

It is a fundamental principle of quantum mechanics, which states that certain pairs of physical properties can’t be measured simultaneously with arbitrary precision, for example a particle’s position and momentum. The properties which can form such pairs are called conjugate properties to each other. In the coming sections we will discuss more about them. In fact the product of uncertainties of the conjugate properties is bounded below. If the conjugate properties are $A$ and $B$, and the standard deviation or uncertainties in their simulaneous measurement in a given experiment are $\sigma_A$ and $\sigma_B$, then

\[ \sigma_A \sigma_B \ge \frac{h}{4\pi} \]

where $h$ is Plank’s constant.

State as an abstract vector#

In everyday life we use the term state when we refer to the situation/condition somebody or something is in. We make it more comprehensive by adding adjectives to it, such as in state of weakness, in state of pain, etc. In case of a physical system, the same idea extends to a comprehensive definition, with quantifiability. The state of a physical system refers to something that can provide complete physically accessible information about the system at a given instant of time. This is quantified with first determining the number of independent quantities required for complete information, and then assigning a variable for each of those. A numerical value of each of those variable defines the state of the system. Formally -

A state is a set of variables describing a system which does not include anything about its history.

This set of variable is assumed to be minimal so that removing any component results in only partial information about the system. Take for example the case of a single isolated particle. Then it’s position and velocity are two independent minimal properties. If the motion of this particle is constrained along a line, then a variable $x$ denoting it’s distance from a chosen origin on the line completely determines it’s position, and it’s time derivative $v = \frac{dx}{dt}$ determines the velocity. Thus together, $(x, v)$ define the state of the particle. If the motion was not constrained, one would need three coordinates $(x, y, z)$ for position, and three components of velocity $(v_x, v_y, v_z)$ with respect to a given reference frame. Thus collectively a set of six variables $(x, y, z, v_x, v_y, v_z)$ defines the state of a particle. For a system of many particles, the variables are concatenated, and the set becomes bigger. For $N$ particle system, the set contains $6N$ variables.

Note that this set has to be ordered so there is no confusion in the meaning of each of its elements. Such ordered sets are essentially what one calls vectors. We discuss vectors in more details in the coming sections.

Add Figure

Degrees of Freedom

The degrees of freedom of a system is a number associated with it. It is the number of independent ways one can change the system’s state. Alternatively, it’s also the minimum number of individual quantities required to specify the state.

In case of single particle, it’s degrees of freedom is 6. For a system of $N$ particles, it’s $6N$.

Now consider a quantum particle, and think whether we can use the above mentioned set of positions and velocities/momenta $(x, y, z, v_x, v_y, v_z)$ can describe the state of quantum particle. Due to uncertainty principle, we immediately run into a problem, because the position $x$, and velocity $v_x$ can not be accurately determined simultaneously. Thus the set of position and velocity variables can not provide complete information about particle’s state.

So how do we define state of a quantum system? Here one postulates, that it is possible to define a state of a quantum system, represented as some type of abstract object. This object will likely have multiple components associated with it, one for each degree of freedom. It will thus be a vector of some kind. For the moment we call it an abstract vector, as we don’t know it’s structure. As we go throught the sections, we will explore how this structure emerges, and how it works.

So, for the moment, we say that the state of a quantum system is represented by an abstract vector. In due course we will learn several synonyms for this abstract vector defining the state of a quantum system.

Superposition principle#

Superposition, issentially means applying multiple effect/stimuli/attributes on a system/object.

In general, the superposition principle applies to anywhere more than one attributes can be imposed on a single object. Formally speaking, the principle states that in all linear systems, the net response caused by two or more stimuli on a system is sum of the individual responses that would have been caused by each individual stimulus.

The sum of responses of individual effects, is same as the response of the sum of individual effecs.

Once we go through the mathematical structure in the coming sections, it will become clear that the superposition principle issentially is a consequence of linearity in the system, or linear behaviour.

In quantum mechanics, the superposition applies to states. What that means is, that if a system can exist in say two states $A$ and $B$, then it can also exist in a superposition of $A$ and $B$. In the section below we will learn how to interpret such a thing mathematically, but for now we can intuitively speculate, that a superposition of two states should have properties resembling both the states even though the two state might be very different.

Figure for illustration

Role of interference#

The notion of intereference is quantum systems is very similar to what it means in waves. When two waves are combined, their instantaneous intensities or displacements are added. The intensity or displacement of the resulting wave can be greater or lower depending on their relative phase.

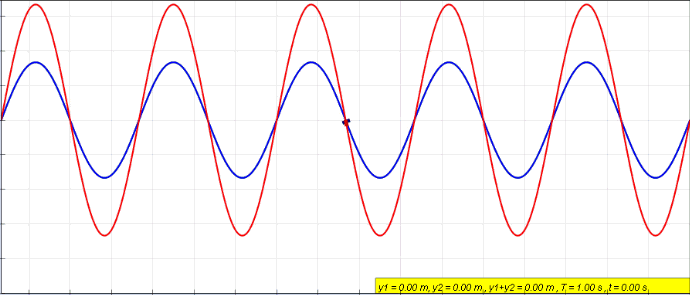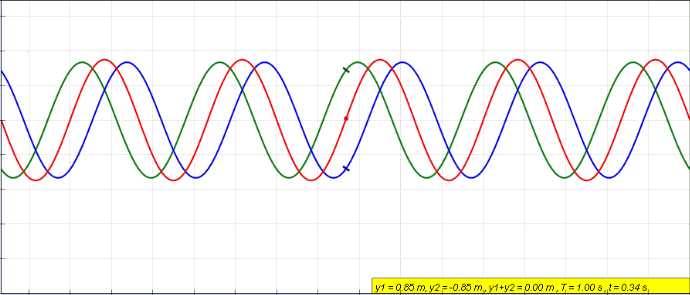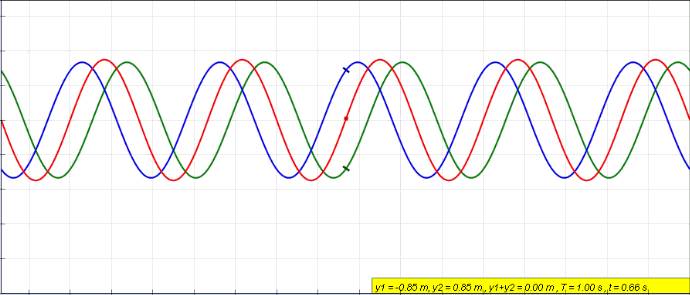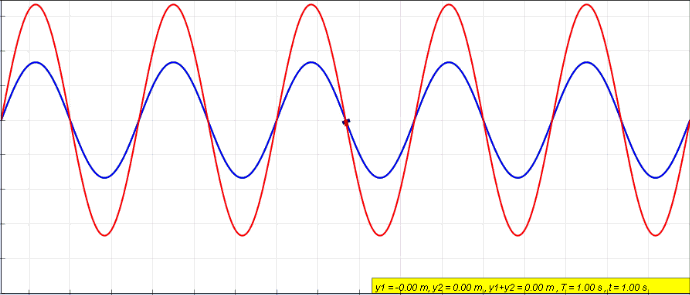
In case of quantum system, as we will see, probability amplitudes take the role of intensity or displacements.

Principles of measurement#

In quantum mechanics, a measurement is testing or manipulation of a physical system that yields a numerical result. This in principle doesn’t look much different than a measurement of a classical system. However, in the quantum realm, the process of measuring something also changes the underlying system.

No-cloning#

Classically we can copy an unknown bit using the following simple process:

We receive an unknown bit. This means we don’t know its state. We don’t know if it is 0 or 1.
Measure the bit and record the outcome. We either get 0 or 1. Say for example we obtain 1.
Using this information, prepare a new bit matching the original bit.
Now we have 11, i.e. the original bit plus a copy.

What happens if we try to copy a qubit using this procedure?

We receive an unknown qubit. We don’t know its state, $\psi=\alpha\ket{0}+\beta\ket{1}$. We don’t know the coefficients $\alpha$ and $\beta$.
Measure the qubit and record the outcome. We either get 0 or 1. Say for example we obtain 1.
We cannot prepare a new qubit matching the old one! We still don’t know 𝛼 and 𝛽.
Plus the original qubit is now destroyed!

There is no process to copy an unknown qubit. This is a consequence of the no-cloning theorem, which is stated as follows:

“An unknown quantum state cannot be precisely recreated, it cannot be cloned”.

Two important words are written in bold in the above theorem:

Unknown: Known states can be copied infinitely many times, simply by repeating the known algorithm used to prepare them
Precisely: Approximate cloning is possible, by taking thousands of measurements in different bases [Bužek & Hillery, PRL 81 22 (1998)].

Entanglement#

Consider the Hilbert space over two subsystems $A$ and $B$, written as $=\mathcal{H}_A\otimes\mathcal{H}_B$. A general state of $\mathcal{H}$ is given by $$ \ket{\psi}_{AB}=\sum_{ij}c_{ij}\ket{i}_A\ket{j}_B. $$

If $\ket{\psi}_{AB}$ can be written as $\ket{x}_A\cdot\ket{y}_B$ then $\ket{\psi}_{AB}$ is separable.
If $\ket{\psi}_{AB}$ cannot be written as $\ket{x}_A\cdot\ket{y}_B$ then $\ket{\psi}_{AB}$ is entangled.

Entangled systems share a quantum state. A measurement performed on one subsystem instantaneously changes the state of the other subsystem, no matter how far apart they may be. Einstein called this ‘spooky action at a distance’.

Tunnelling#

Tunneling is a phenomenon that can occur when a quantum particle approaches a potential barrier (this could be gravitational potential, electrical potential, etc.)

In the classical case, if the energy of the barrier is $U$ and the energy of the particle is $E$,

the particle is transmitted through the barrier if $E>U$
the particle is reflected if $E<U$.

In the quantum case things get more interesting.

Quantum systems display both particle-like and wave-like behaviour. Quantum particles can be partially transmitted and partially reflected.
There is a non-zero probability of finding the quantum particle beyond the classically insurmountable barrier!
I.e., the quantum particle may tunnel through the barrier even if $E<U$.
The probability of this tunnelling taking placew decreases exponentially with the width of the barrier.

Dirac Notation#

\[ {\Huge \left\langle \text{Bra}| \text{Operator}| \text{Ket} \right\rangle = \text{Number} }\]

The Dirac notation, also called Bra-Ket notation, is a notation used in Quantum Physics to express vector operations, and inner product. It makes interpretation of state, observations and inner product easier.

It uses angular brackets $\langle , \rangle$ and vertical bar $|$.
A Ket is a vector of the Hilbert space denoted as $|v\rangle$, and represents state of a quantum system.
Action of linear operator $A$ on a ket is expressed as $A|v\rangle$.
A Bra is of the form $\langle f|$. It is a map $f: V\longrightarrow C$, i.e., it maps a vector to a number, usually complex number.
With an inner product $\langle , \rangle$ defined on vector space, each ket has a unique corresponding bra $\langle v, ~ \rangle \equiv \langle v|$
Basically a bra is a map that is literally parameterised by the vector of Hilbert space, and its action on a vector is governed by the defined inner product.
The inner product then is equivalently expressed more conveniently as

\[ \langle v_1, v_2 \rangle \equiv \langle v_1 | v_2 \rangle , \quad\text{and for some operator, }A\quad \langle v_1, A v_2\rangle \equiv \langle v_1|A|v_2\rangle \]

The set of all Bra is called dual space of vector space, and both can be used to represent the state.
One also defines outer product, of two vectors as $L=|v_1\rangle \langle v_2|$, which acts as an operator $L(v)\equiv L|v\rangle = |v_1\rangle\langle v_2|v\rangle = \langle v_2|v\rangle|v_1\rangle$. Here applying $L$ on $|v\rangle$ gives the state $|v_1\rangle$ multiplied by scalar $\langle v_2|v \rangle$.
For a basis $\{|v_1\rangle, |v_2\rangle, \dots, |v_n\rangle \}$ there is a corresponding basis for dual space, a basis of bra’s $\{\langle v_1|, \langle v_2|, \dots, \langle v_n|\}$
The linear combination for a ket is simply expressed as $|v\rangle = \sum_i a_i |v_i\rangle$, however, for the corresponding bra $\langle v|$ has conjugate coefficients.

\[ \langle v| = \sum_i a_i^*\langle v_i| \]

States and Operators#

Here we will recall the fundamental notions of quantum mechanics we use when we setup the mathematical framework for a given quantum system.

To describe or study a quantum system, we first start with a set of states that are mutually exclusive with respect to an observation or measurement. Classically, a system and observations are two distinct things without their interplay. Since classically when we observe something, for example a moving car, or a passing meteor, our ‘observation’ does not affect the dynamics or behaviour of the system in question. It is because the interaction of the observer and the system is usually so weak that there is no effect of the presence of observer on the system.

But within the quantum realm, this is not the case. In the strict sense, any observation in quantum realm is result of a measurement, which itself is associated with the property of the system, such as position, momentum, or energy of the system. Secondly, in the quantum realm, properties are quantised, that is, instead of any possible value, there exist descrete values or outcomes that individual measurement can result in. For example, in case of a qubit, the measurement of the state result in either $|0\rangle$ or $|1\rangle$.

So when there is an observation we think of, and the decrete set of state the system is in, and these state are mutually exlusive in the sense of possibility.

If the system is found in one of those state, and the corresponding measurement is done, it will always be found in that state. We choose this set as our basis. Imagine there are $n$ possible states, then basis may be expressed as $B=\{|1\rangle, |2\rangle, |3\rangle, \dots, |n\rangle\}$. Here the states are symbolically expressed by the outcome labels $1, 2, \dots, n$. The Hilbert space for the quantum system is then the linear span of these states -

\[ H_b = \left\{|s\rangle =\sum_{l=1}^n c_l|l\rangle: \text{where } c_l\in \mathbb{C}\right\} \]

Each vector in this Hilbert space is a possible state. This is because of the superposition principle which states that If a quantum system can exist in two states (or more), it can exist in all possible superpositions of the two (or more of those) states. Let’s see below what this superposition means in connection with a quantum system.

Connection with Experiment#

We have the following probabilistic interpretation of a general state in the Hilbert space.

Probabilistic interpretation#

Probabilistic interpretation of superposition

The coefficients $c_l$ are complex probability amplitudes for each state $|l\rangle$, and the actual probability of measurement outcome being in the state $|l\rangle$ is $|c_l|^2$. Since sum of all the probabilities must add to 1, we must have -

\[ 1 = \sum_{l=1}^n |c_l|^2 = |c_1|^2 + |c_2|^2 + \dots +|c_n|^2 \]

Overlap of probability

The inner product of the two states $\langle s, s'\rangle \equiv \langle s|s'\rangle$ gives the overlap of probabilities of the two states.

For mutually exclusive states this overlap is zero, hence the mutually exclusive states should be orthogonal to each other. That is why we impose that the basis above is orthogonal, i.e., $\langle l|l'\rangle = 0$ for $l\ne l'$ and normal $\langle l|l\rangle = 1$.

Further, lets compute the norm of the above generic state $|s\rangle$.

\[ \langle s|s\rangle = \sum_l c_l^*\langle l| \sum_{l'} c_{l'}|l'\rangle = \sum_{l,l'} c_l^*c_{l'}\langle l|l'\rangle = \sum_{l} |c_l|^2 \]

But the probability argument implied that the last summation equals 1, so $\langle s|s'\rangle = 1$, that is the norm of the state must also be 1. That is why in quantum system, a state is represented by a unit vector of the Hilbert space.

Interpretation of measurement#

Let us try to illustrate how quantum measurement works. When we measure a property of a quantum system, the outcome of the measurement should yield a value.

Let’s assume the quantum system imagined in the previous section, the states are $|l\rangle$ with $l=1,2,\dots n$. If the system is already in one of these states, then it stays in it, and the outcome of the measurement is, say $a_l$ corresponding to the state $|l\rangle$.

This observation, against our intuition of uncertainty in quantum system, is actually definite. Is there something special about the system being in state $|l\rangle$ ? Yes, it is so because these state are by construction mutually exclusive with respect to observation, as discussed in section states-and-operators.

The uncertainty comes if before the measurement system was in a superposition state $|s\rangle = c_1|1\rangle + c_2|2\rangle + \dots c_n|n\rangle$. In this case, the system is in a state where the possibility of being in any one of the $|l\rangle$ state coexist until the measurement.

Once we observe the system, or measure it, the system collapses into one of the $|l\rangle$ states with probability $|c_l|^2$. In this situation the outcome is not definite, but probabilistic, and if we repeat the above experiment, we get a probability averaged outcome, called expectation value. It is denoted as $\langle a \rangle$ and is given by the weighted average of the probabilities -

\[ \langle a \rangle = \sum_{l=1}^n |c_l|^2 a_l \]

Mathematical interpretation#

Mathematically, the above measurement is interpreted as following.

Every physically measurable quantity is called an observable, and for every observable, there is a Hermitian operator, say $A$ that acts on a state. If the state is $l\rangle$, the result of the action is $A|l\rangle=a_l|l\rangle$, and if the state is in superposition $|s\rangle$, the state changes to $A|s\rangle$.

The overlap, or inner product of the resulting state with initial state gives the outcome of the measurement. The outcome, which is also called the expectation value, is expressed as $\langle s, As\rangle$ or $\langle s|A|s\rangle$ in the Dirac notation.

For the $|l\rangle$ state, the outcome is $\langle l|A|l\rangle = a_l\langle l|l\rangle = a_l$, and if definite.
For the superposition state, the outcome is probabilistic with expectation value

\[\begin{split} \begin{align*} \langle a \rangle &= \langle s|A|s \rangle = \left( \sum_{l'}c_{l'}^*\langle l'| \right)A \left( \sum_l c_l|l\rangle \right)\\ &= \sum_{l,l'}c_{l'}^*c_l a_l\langle l'|l \rangle = \sum_l a_l|c_l|^2 \end{align*} \end{split}\]

which is same as one interpreted as measurement outcome in the previous section.

Measurement in the computational basis#

The Born rule tells us that if we measure a generic qubit state, $\psi=\alpha\ket{0}+\beta\ket{1}$, in the computational basis, $\{\ket{0},\ket{1}\}$, the probability of outcome 0 is given by

\[\begin{split}\begin{align*} P(0)&=|\langle0|\psi\rangle|^2\\ &=|\bra{0}\left(\alpha\ket{0}+\beta\ket{1}\right)|^2\\ &=|\langle0|\alpha|0\rangle+\langle0|\beta|1\rangle|^2\\ &=|\alpha\langle0|0\rangle+\beta\langle0|1\rangle|^2\\ &=|\,\alpha\cdot1+\beta\cdot0\,|^2 \\ &=|\alpha|^2. \end{align*} \end{split}\]

Via similar working we can calculate that the probability of outcome 1 is given by

\[ P(1)=|\langle1|\psi\rangle|^2=|\beta|^2. \]

Measurement in a different basis#

We can generalise the above procedure to account for measuring a state $\ket{\psi}$ in any basis $\{\ket{b_i}\}$. Each possible measurement outcome corresponds to a projector,

\[ P_i=\ket{b_i}\bra{b_i}. \]

The probability of outcome $i$ is

\[\begin{split} \begin{align*} P(i)&=\langle\psi|P_i|\psi\rangle\\ &=\langle\psi|b_i\rangle\langle b_i|\psi\rangle\\ &=|\langle b_i|\psi\rangle|^2, \end{align*} \end{split}\]

where in the final line we have used the fact that $\langle b_i|\psi\rangle$ is the complex conjugate of $\langle\psi|b_i\rangle$, and a complex number multipled by its own complex conjugate gives the square of its magnitude,

\[ z\cdot z^*=|z|^2, \; z\in\mathbb{C}. \]

Hilbert space of Qubits#

Let us finally come to example of quantum systems that are useful for quantum computing.

Single Qubit#

A Qubit is a quantum system with two state basis. A single qubit is one of the simplest quantum system of 2-dimensional Hilbert space.

A qubit is an abstraction of a quantum system with two dimensional Hilbert space, with a basis $\{|0\rangle, |1\rangle\}$. The Hilbert space then looks like

\[ H_1 = {|s\rangle = c_0|0\rangle + c_1|1\rangle: c_0, c_1 \in \mathbb{C}} \]

Note that in order to represent a quantum state, the kets $|s\rangle$ need to be normal, which means

\[ |c_0|^2 + |c_1|^2 = 1 \]

Since the Hilbert space is two dimensional, all the operator on it can be represented as $2\times 2$ complex matrices.

Noteworthy operators are the following -

Identity $I$, and Hadamard $H$ operators. Their matrix representation is following -

\[\begin{split} I = \begin{pmatrix} 1 & 0\\0 & 1 \end{pmatrix}; H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1\\1 & -1 \end{pmatrix} \end{split}\]

Pauli $X, Y, Z$ operators. Their matrix representation is following - $$ X = \begin{pmatrix} 0 & 1\\1 & 0 \end{pmatrix}; Y = \begin{pmatrix} 0 & -i\\i & 0 \end{pmatrix}; Z = \begin{pmatrix} 1 & 0\\0 & -1 \end{pmatrix}; $$

One assumes a coordinate system with $x,y$ and $z$ axis, and a basis that is eigenstate of Pauli z operators.

Multiple Qubits#

In general, when we combine two quantum systems, the Hilbert space of the combined system is constructed from the cartesian product of the basis of component systems.

Let us first consider a system of two qubits, if the basis for one qubit is $B_1 = \{|0\rangle, |1\rangle\}$, then the basis for the two qubit system is

\[ B_2 = B_1\times B_1 = {(|0\rangle, |0\rangle), (|0\rangle, |1\rangle), (|1\rangle, |0\rangle), (|1\rangle, |1\rangle)} \]

Where the order of the states in ordered pair follows the qubit label. For example, $(|0\rangle, |1\rangle)$ represents a state in which first qubit is in 0 state, and second qubit is in 1 state.

If we have more qubits, the Hilbert space will grow as $B_3 = B_1\times B_1\times B_1$, and so on. The ordered pair notation becomes combersome, so one puts the individual state labels inside the angular brackets. In this way, the basis for two and three qubits looks like following -

\[\begin{split} \begin{align} B_2 = &\{|00\rangle, |01\rangle, |10\rangle, |11\rangle\}\\ B_3 = &\{|000\rangle, |001\rangle, |010\rangle, |011\rangle, |100\rangle, |101\rangle, |110\rangle, |111\rangle\}\\ B_4 = &\{ |0000\rangle, |0001\rangle, |0010\rangle, |0011\rangle,\\ &|0100\rangle, |0101\rangle, |0110\rangle, |0111\rangle,\\ &|1000\rangle, |1001\rangle, |1010\rangle, |1011\rangle,\\ &|1100\rangle, |1101\rangle, |1110\rangle, |1111\rangle \} \end{align} \end{split}\]

Tip

The size of the basis, and hence the dimension of the Hilbert space of $n$ qubits is $2^n$

Pure vs Mixed States#

Pure state#

The quantum state we referred to so far are what one calls pure states, and they are represented by a normalised vector in a complex Hilbert space. In the Dirac notation, they are described as a ket $|v\rangle$ or a bra $\langle v|$.

There is another way to describe the state of quantum system which can be generalised to mixed states (defined below), and the is through density operator. For a system in pure quantum state $|v\rangle$, the density operator is defined as

\[ {\Huge \rho = |v\rangle \langle v| } \]

It is easy to see that trace of the density operator is 1, i.e., $\text{Tr}(\rho)=1$.
For a pure state, $\rho^2 = \rho$, so $\text{Tr}(\rho^2)=1$

Mixed state#

Suppose we have a quantum system, and wish to prepare it in a state $|l\rangle$ out of, say $\{|1\rangle, |2\rangle, |3\rangle,\dots, |n\rangle\}$. If we could do it, then the system is in a pure state. But on the other hand, due to some difficulty, experimental or otherwise of physical nature, when we try to prepare it in $|l\rangle$, each time we get the system prepared in a different state. We can repeat the attempt of preparing the state several times, and compute the statistical weight $w_l$ of having prepared the system in the expected state $|l\rangle$. This adds another uncertainty, which is classical in nature on any measurement on the system in such a state, and any outcome of quantum measurement will be an ensemble average of these weights. Such a state is called a mixed state.

What mathematical object should we use to represent such a state? Clearly a single vector does not suffice, so we need something that depends on the weights $w_l$ and the state $|l\rangle$ for all values of $l$.

Such state are represented by the following

\[ \rho = \sum_l w_l |l\rangle \langle l| \]

For a mixed state, $\rho^2 \ne \rho$, and $\text{Tr}(\rho) <1$.

Interactive Qubit State Visualization#

Below we show an interactive illustration how a qubit is visualized on a Bloch sphere. An arbitrary qubit can be expressed in terms of two angles $\theta, \phi$, which are mapped to unit vectors in 3D as follows

\[\begin{split} |\theta, \phi\rangle = \begin{pmatrix} \cos{\frac{\theta}{2}}\\ e^{i\phi}\sin{\frac{\theta}{2}} \end{pmatrix} \longleftrightarrow \begin{pmatrix} \sin{\theta}\cos{\phi}\\ \sin{\theta}\sin{\phi}\\ \cos{\theta} \end{pmatrix} \end{split}\]

The interactive widget below lets you move the $\theta, \phi$ on the plane to show how the corresponding point on the Bloch sphere moves with it.

Use the controls on the left to drag the state and the mouse to rotate the 3D sphere.